[文献阅读] Multi-Agent Deep Reinforcement Learning for Computation Offloading and Interference Coordination in Small Cell Networks 用于小蜂窝网络计算卸载和干扰协调的多智能体深度强化学习

发表于 2022-05-21 更新于 2022-07-12 收录于文献阅读

sci-2。使用部分卸载。考虑的是蜂窝网络的环境，使用多智能体强化学习(DRL)的方法最小化延迟。为了降低训练过程的计算复杂性和开销，引入了联邦学习，设计了一个联邦DRL方案。

摘要与主要贡献

期刊：IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY.2021.

缩写：小型蜂窝基站(SBS) 用户设备(UE)

主要研究小蜂窝网络的分布式智能计算卸载和干扰协调方案。重点研究了基于MARL的多用户多小区网络中计算卸载、信道分配、功率控制和计算资源分配的联合优化问题。

论文贡献：
将联合计算卸载和干扰协调问题作为多智能体DRL问题，最小化系统能耗。
提出了一种基于分布式多智能体DRL的计算卸载和资源分配方法。
为了减少训练过程的计算复杂度和开销，提出了一种基于DRL的联邦计算卸载和资源分配方法。它只需要SBS代理共享其模型参数而不是本地训练数据。

系统模型

支持边缘智能的小型蜂窝网络

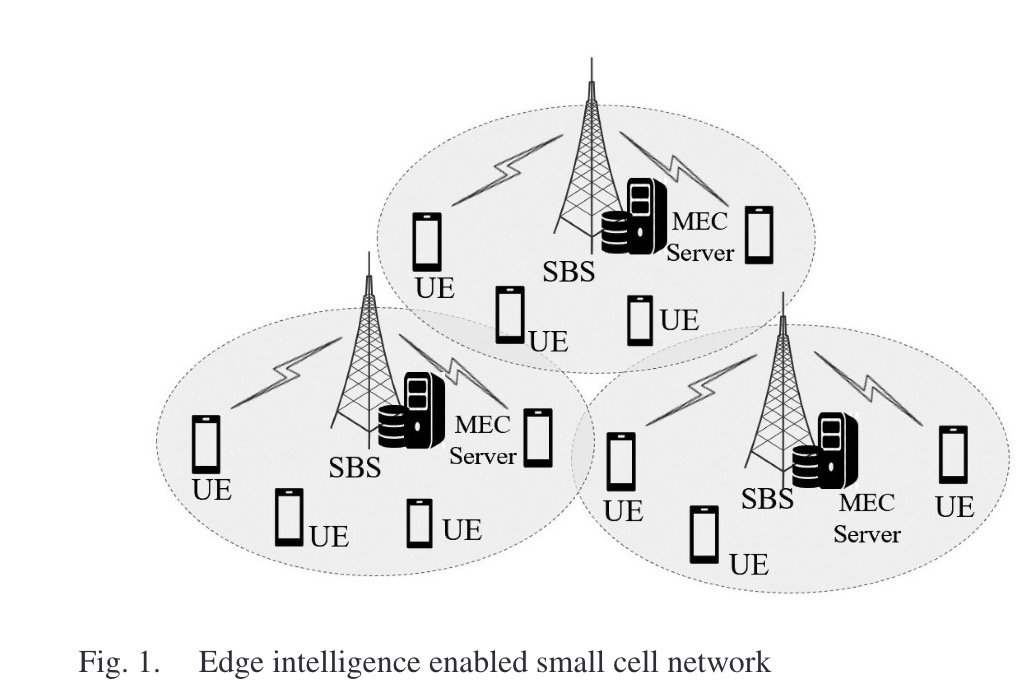
如图1所示，由随机分布的SBS和非随机分布的UE组成。SBS配备了MEC服务器，表示为$\mathcal{M}={0,1,2,…M}$，用户和SBS的集合为$m \in \mathcal{M}, \mathcal{N}_m={1,2,…,N_m}, \sum_m| \mathcal{N}_m |=N$。
边缘服务器m中的用户n的任务可以表示为$Task_n^{(m)}=\{d_n^{(m)}, \omega_n^{(m)},\tilde{T}_n^{(m)}\}$, $d_n^{(m)}$ 表示任务的大小， $\omega_n^{(m)}$ 表示完成计算任务所需要的计算能力(CPU周期)， $\tilde{T}_n^{(m)}$ 表示UE可以容忍的最大延迟。
考虑的是部分卸载。

通信模型

定义 $\alpha_n^{(m)} \in [0,1]$ 为卸载比例。具体的， $\alpha_n^{(m)}d_n^{(m)}$ 为在边缘服务器上计算的任务大小，$(1-\alpha_n^{(m)})d_n^{(m)}$ 为在本地计算的大小。
K表示系统中的正交信道，不同区域之间存在同频干扰，在每个区域内，采用正交频分多址方法，即不会有干扰。定义 $b_{n,k}^{m} \in \{0,1\}$ 作为m的信道指示器。$b_{n,k}^{(m)}=1$表示m将信道k分配给m，反之$b_{n,k}^{(m)}=0$。SBS的信道分配决策满足约束$\sum_{n \in \mathcal{N}_m}b_{n,k}^{(m)} ≤1,\forall k \in \mathcal{K}, m \in \mathcal{M}$。此外，假设每个UE卸载任务时可以在最长的信道进行分配，即$\sum_{k \in \mathcal{K}_m}b_{n,k}^{(m)} ≤1,\forall n \in \mathcal{N}_m, m \in \mathcal{M}$。
定义 $p_n^{(m)} \in [0,P_n^{(m),max}]$ 为n向m的传输功率，$P_n^{(m),max}$是m的最大传输功率。因此，当用户n卸载任务到边缘服务器m上时，在信道k上的上行链路的速率为：

r_{n, k}^{(m)} = B \log_{2} (1 + \frac{p_{n}^{(m)} h_{n, k}^{(m)}}{N_{0} B + I_{k}^{(m)}})

B为信道带宽，$h_{n,k}^{(m)}$为信道增益，$N_0$为噪声，$I_k^{(m)}=\sum_{m^{‘}≠m}\sum_{n^{‘} \in \mathcal{N}_{m^{‘}}},P_{n^{‘}}^{(m){‘}}g_{n{‘},k}^{(m)}$为干扰信道增益。

因此，n到m的上行链路速率为：
$U_n^{(m)}=\sum_{k \in \mathcal{K}}b_{n,k}^{(m)}r_{n,k}^{(m)} $
我们可以得知上行链路速率不仅取决于分配的信道和其自身的发射功率，还取决于其他区域中卸载UE的干扰。从系统优化的角度来看，不同区域之间的计算卸载、信道分配和功率控制的协调对于缓解小区间干扰从而提高卸载性能至关重要。

计算模型

本地计算

设CPU频率为 $C_n^{(m)}$ ,本地计算的时间为：
$LocT_m^{(m)}=(1-\alpha_n^{(m)})\omega_n^{(m)}/C_n^{(m)} $
$\varepsilon_n^{(m)}$为能耗系数，本地计算的能耗为：
$LocE_n^{(m)}=(1-\alpha_n^{(m)})\omega_n^{(m)} \varepsilon_n^{(m)} $

边缘计算

给定卸载比例 $\alpha_n^{(m)}$，可以得到传输到SBS的传输时延和传输能耗为：$OffT_n^{(m),tr}=\alpha_n^{(m)}d_n^{(m)}/U_n^{(m)} $ $OffE_n^{(m),tr}=p_n^{(m)}\alpha_n^{(m)}d_n^{(m)}/U_n^{(m)} $

SBS上边缘服务器的计算能力为 $\bar{C}^{(m)}$ 。对于卸载到m的移动设备n，定义 $f_n^{(m)} \in (0,1]$ 为n分配到的资源。因此在边缘服务上的计算时延和计算能耗为：$OffT_n^{(m),ex}=\alpha_n^{(m)} \omega_n^{(m)}/f_n^{(m)} \bar{C}^{(m)} $ $OffE_n^{(m),ex}=\alpha_n^{(m)} \omega_n^{(m)} \bar{\varepsilon}^{(m)} $

其中$\bar{\varepsilon}^{(m)} $为能耗系数。

可以得到总时延和总能耗为：$OffT_n^{(m)}=OffT_n^{(m),tr}+OffT_n^{(m),ex}$ $OffE_n^{(m)}=OffE_n^{(m),tr}+OffE_n^{(m),ex}$

多智能体DRL计算卸载和资源分配模型

将一个调度周期设为一个时隙，每个时隙的计算卸载和资源分配问题表述如下： $\begin{aligned} P 0 : min_{α [t], b [t], p [t], f [t]} \sum_{m} \sum_{n} ({LocE}_{n}^{(m)} [t] + O f f E_{n}^{(m)} [t]) \\ s . t . \\ C 1 : max {Loc T_{n}^{(m)} [t], O f f T_{n}^{(m)} [t]} ⩽ {\tilde{T}}_{n}^{(m)}, \forall m, n \\ C 2 : α_{n}^{(m)} [t] \in [0, 1], \forall n, m \\ C 3 : b_{n, k}^{(m)} [t] \in {0, 1}, \forall n, m, k \\ C 4 : \sum_{k \in K} b_{n, k}^{(m)} [t] \leq 1, \forall n, m \\ C 5 : \sum_{n \in N_{m}} b_{n, k}^{(m)} [t] \leq 1, \forall k, m \\ C 6 : p_{n}^{(m)} [t] \in [0, P_{n}^{(m), max}], \forall m, n \\ C 7 : f_{n}^{(m)} [t] \in (0, 1], \sum_{n \in N_{m}} f_{n}^{(m)} [t] \leq 1, \forall m \end{aligned}$

$\pmb{\alpha}[t]={\alpha_n^{(m)}[t]},\pmb{b}[t]={b_{n,k}^{(m)}},\pmb{p}[t]={p_n^{(m)}[t]},\pmb{f}[t]={f_n^{(m)}[t]}$。

约束C1保证计算任务的延迟要求。C2表示任务卸载百分比。C3-C5表示每个UE最多可以分配一个信道，每个区域中的每个信道最多分配给一个UE。C6表示每个UE的传输功率约束。C7表示分配给每个UE的计算资源不能超过每个单元中MEC服务器的可用资源。
使用DRL来解决此全局优化问题。

多智能体环境

让SBS当Agent，让其与环境交互。
- State：在现实环境中，让S[t]包含全局信道状态和所有SBS Agent的行为是不现实的，他们只能观测到部分环境。在本文中，Agent m能观测到每个信道上自身信号链路的本地信号增益、每个信道SBS m接收到的干扰功率，以及其覆盖的UE的任务配置。 $s_m[t]=\{\pmb{h}_m[t],\pmb{I}_m[t],\pmb{Task}_m[t]\}$
  - $\pmb{h}_m[t]={[h_{1,1}^{(m)}[t],…,[h_{1,K}^{(m)}[t]],…,[h_{|\mathcal{N}_m|,1}^{(m)}[t],…,h_{|\mathcal{N}_m|,K}^{(m)}[t]]}$ 表示n到m的在信道k上的瞬时增益。
  - $\pmb{I}_m[t]=[I_1^{(m)}[t],…,I_K^{(m)}[t]]$ 表示m接收到的干扰功率。
  - $\pmb{Task}_m[t]=[Task_1^{(m)}[t],…,Task_{|\mathcal{N}_m|}^{(m)}[t]]$ 表示m对UE的配置文件。
- Action Space:在每个时隙t中，Agent m根据其观测做出动作。其动作包括计算卸载决策、信道分配、上行链路功率控制和计算资源分配。 $a_m[t]=\{\pmb{\alpha}_m[t],\pmb{b}_m[t],\pmb{p}_m[t],\pmb{f}_m[t]\}$
  - $\pmb{\alpha}_m[t]=[\alpha_1^{(m)}[t],…,\alpha_{|\mathcal{N}_m|}^{(m)}[t]]$ 表示计算卸载决策。
  - $\pmb{b}_m[t]={[b_{1,1}^{(m)}[t],…,[b_{1,K}^{(m)}[t]],…,[b_{|\mathcal{N}_m|,1}^{(m)}[t],…,b_{|\mathcal{N}_m|,K}^{(m)}[t]]}$ 表示分配给每个UE用于将卸载任务传输给m的信道。
  - $\pmb{p}_m[t]=[p_1^{(m)}[t],…,p_{|\mathcal{N}_m|}^{(m)}[t]]$ 表示UE n上行链路的传输速率。当$p_n^{(m)}[t]=0$时表示此任务在本地计算。
  - $\pmb{f}_m[t]=[f_1^{(m)}[t],…,f_{|\mathcal{N}_m|}^{(m)}[t]]$ 表示SBS m分给每个UE n的计算资源，当$f_n^{(m)}[t]=0$时表示此任务在本地计算。
- Reward:目标是最小化能耗，定义即时能耗为：
  $\begin{array}{l} R_{m}^{C o} [t] \\ = \sum_{m \in M} \sum_{n \in N_{m}} (- L o c E_{n}^{(m)} [t] - O f f E_{n}^{(m)} [t] + V_{n}^{(m)} [t]) \end{array}$
  
  -总能耗+剩余时间
  
  其中$V_n^{(m)}[t]$为：
  $V_{n}^{(m)} [t] = G ({\tilde{T}}_{n}^{(m)} - max {Loc T_{n}^{(m)} [t], O f f T_{n}^{(m)} [t]})$
  
  n可以忍受的最大延迟-max(本地计算时间，卸载边缘服务器的总计算时间)
  
  其中$G(x)$为分段函数。例如：当$x≥0$时，$G(x)=\beta$，其他情况$G(x)=x$.$V_n^{(m)}[t]$为一个常数，$\beta$，当计算任务的延迟达到要求时为受益，否则为负惩罚，绝对值等于延迟要求与执行计算任务所需时间的差值。在实践中，$\beta$为一个超参数，需要调优。agent的学习目标是使折扣奖励最大化，记为：
  $J_{m} = E (\sum_{t = 0}^{\infty} γ^{t} R_{m}^{C o} [t])$

基于MARL的计算卸载于资源分配方案

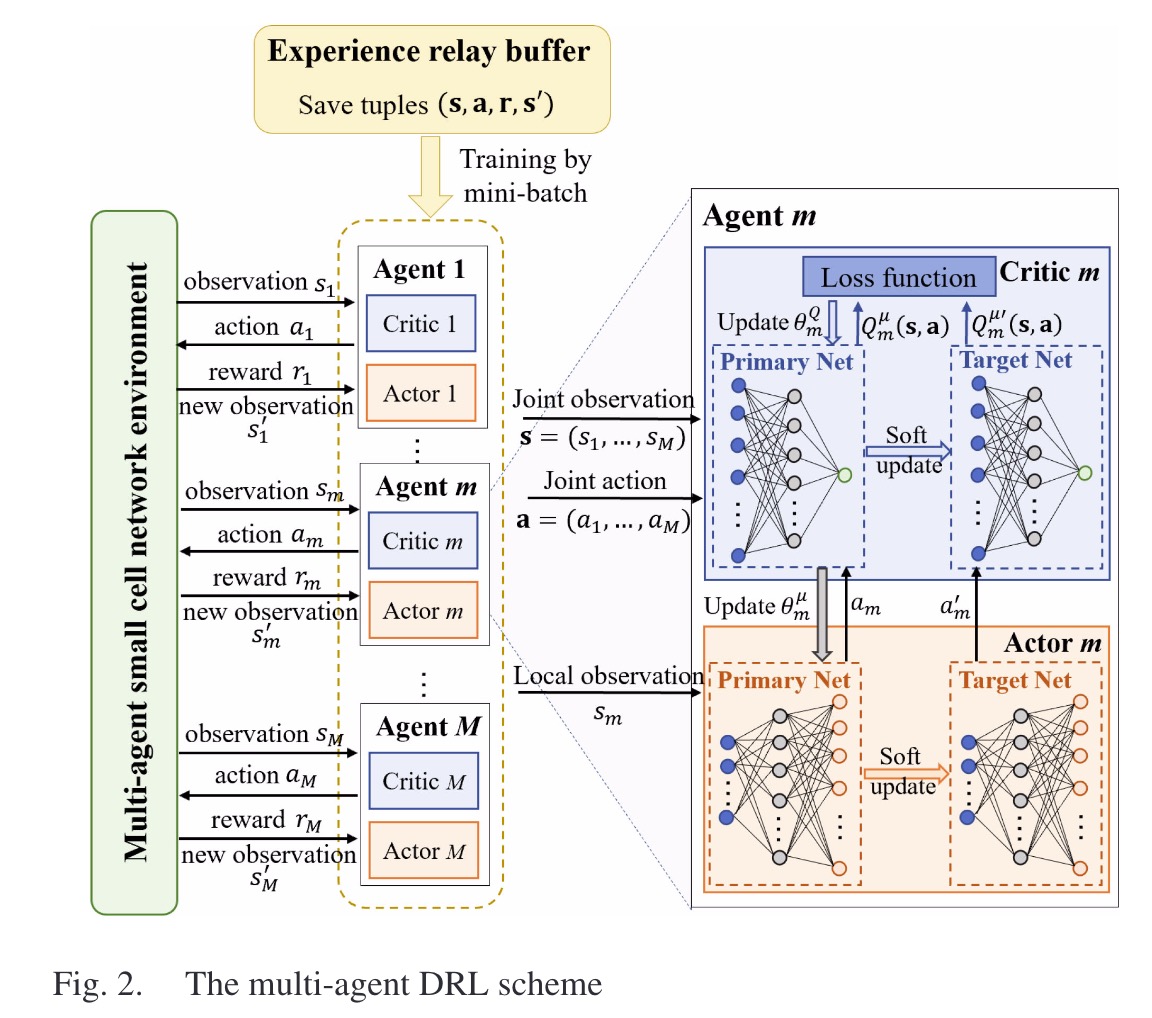
每个Agent都被建模为DDPG。Critic网络输出Q值帮助Actor训练，Actor网络输出动作。且都有一个target网络。
设Actor网络的集合为$\pmb{\mu}=\{\pmb{\mu}_1,…,\pmb{\mu}_M\}$,参数为$\pmb{\theta^{\mu}}=\{\theta_1^{\pmb{\mu}},…,\theta_M^{\pmb{\mu}}\}$。target actor网络为$\pmb{\mu^{‘}}_m$，参数为$\theta^{\pmb{\mu^{‘}}}_m$。
设critic网络的集合为$\pmb{Q}=\{Q_1,…,Q_M\}$,参数为$\pmb{\theta}^{Q}=\{\theta_1^{Q},…,\theta_M^{Q}\}$。target critic网络为$Q^{‘}_m$，参数为$\theta^{Q^{‘}}_m$。
replay buffer中存放的transition为 $(s[t],a[t],r[t],s[t+1])$ ，
其中$s[t]=\{s_1[t],…,s_M[t]\}, a[t]=\{a_1[t],…,a_M[t]\}, r[t]=\{r_1[t],…,r_M[t]\},r_m[t]=R_m^{Co}[t]$。
Loss Function:

L_{m} (θ_{m}^{Q}) = \frac{1}{W} \sum_{j = 1}^{W} [y_{m}^{j} - Q_{m}^{μ} (s^{j}, a_{1}^{j}, . . ., a_{M}^{j})]^{2}

W为batch size，$y_m^j$为target critic估计的目标值，计算公式为：
$y_{m}^{j} = r_{m}^{j} + γ Q_{m}^{μ^{^{'}} μ^{^{'}}} (s^{^{'} j}, a_{1}^{^{'}}, . . ., a_{m}^{^{'}}) |_{a_{k}^{^{'}} = μ μ_{k}^{^{'}} (s_{k}^{j})}$

critic网络更新:
$\theta _m^Q \gets \theta _m^Q - \delta \nabla _{\theta _m^Q}L(\theta _m^Q)$
Actor网络使用policy gradient方式更新：
$\begin{array}{l} \nabla_{θ_{m}^{μ}} J_{m} (θ_{m}^{μ}) = \\ {\frac{1}{W} \sum_{j = 1}^{W} \nabla_{θ_{m}^{μ}} μ (s_{m}^{j}) \nabla_{a_{m}} Q_{m}^{μ} (s^{j}, a_{1}^{j}, ., a_{m}, ., a_{M}^{j}) |}_{a_{m} = μ (s_{m}^{j})} \end{array}$

$\theta^{\pmb{\mu}}_m$参数更新：

$\theta ^\mu _m \gets \theta ^\mu _m - \delta \nabla _{\theta ^\mu _m} J(\theta ^\mu _m)$

target网络参数更新$\theta^{Q^{'}}_m = \tau \theta^Q_m + (1 - \tau)\theta^{Q^{'}}_m $ $\theta^{\pmb{\mu} ^{'}}_m = \tau \theta^{\pmb{\mu}}_m + (1 - \tau)\theta^{\pmb{\mu} ^{'}}_m $

MADRL算法

联邦DRL计算卸载

问题表述

在提出的MARL算法中，需要所有的Agent的观察和动作的全局信息来训练Actor和Critic网络，因此Agent之间需要交换他们的局部信息，这回导致额外的开销。为了减少开销，本文设计了一种用于联邦计算卸载和资源分配的算法。

全局优化问题P0可以分解为M个子问题，每个子问题对应一个小基站。以区域m为例，给定$I_k^{(m)}[t],k \in \mathcal{K}$,局部优化子问题可以公式化为：

\begin{aligned} P 1 : min_{α α_{m} [t], b b_{m} [t], p p_{m} [t], f f_{m} [t]} \sum_{n} (L o c E_{n}^{(m)} [t] + O f f E_{n}^{(m)} [t]) \\ s . t . \\ C 1 - C 7 i n (11) \end{aligned}

$\pmb{\alpha}_m[t]=\{\alpha_n^{(m)}[t]\}, \pmb{b}_m[t]=\{b_{n,k}^{(m)}[t]\},\pmb{p}_m[t]=\{p_n^{(m)}[t]\},\pmb{f}_m[t]=\{f_n^{(m)}[t]\}, n \in \mathcal{N}_m,k \in \mathcal{K}$ 。注意P1也是一个MINLP问题，目标是最小化单元的能耗，而不是所有单元的总能耗。此外，所有的约束只与它本身有关。

可以使用分布式联邦学习来提高各个本地DRL模型的训练性能，而无需集中训练数据。

联邦MARL框架

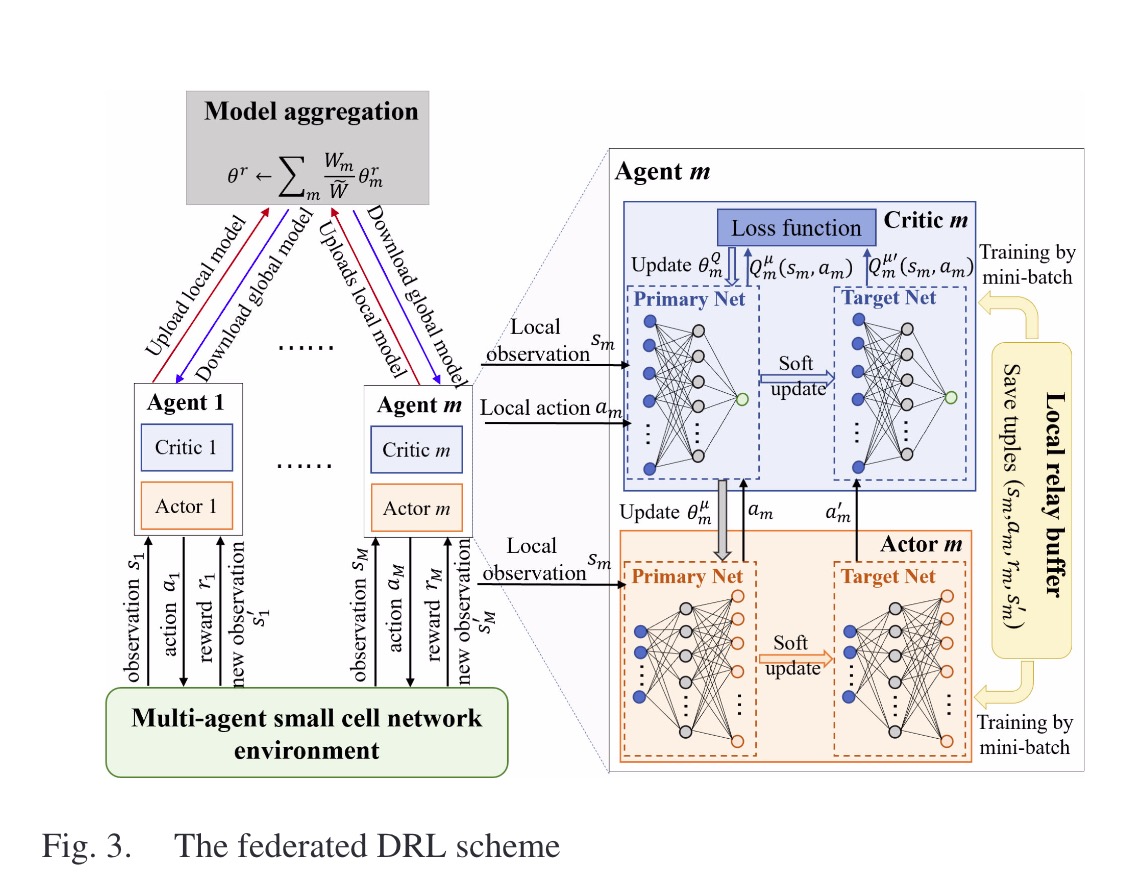
如图所示，每个SBS运行一个本地DDPG模型。根据P1，每个SBS Agent的目标是在满足延迟需求的同时，最小化能耗。m在时隙t中的奖励$R_m^{Fl}[t]$定义为：
$R_m^{Fl}[t]=\sum _{n \in \mathcal{N}_m}(-LocE_n^{(m)}[t]-OffE_n^{(m)}[t]+V_n^{(m)}[t])$
对于Agent，我们定义Actor网络为$\pmb{\mu}_m$，参数为$\theta^{\pmb{\mu^{‘}}}_m$。critic网络为$Q_m$,参数为$\theta^Q_m$。同样有一个replay buffer,transition为$(s_m[t],a_m[t],R_m^{Gl}[t],s_m[t+1])$。
Loss Function：
$L_m^{Fl}(\theta _m^Q)=\frac{1}{W_m}\sum _{j=1}^{W_m}[y_m^j-Q_m^{\pmb{\mu}}(s_n^j,a_m^j)] ^2$

$W_m$为batch size，$y_m^j = R_m^{Fl}+\gamma Q_m^{\pmb{\mu^{‘}}}(s_n^{‘j},a_m^{‘j})|_{a_m^{‘j}=\pmb{\mu}^{‘}_m (s_n^{‘j})}$ 是target critic的目标值。

actor网络使用policy gradient更新： $\begin{array}{l} \nabla_{θ_{m}^{μ}} J_{m}^{F l} (θ_{m}^{μ}) \\ = {\frac{1}{W_{m}} \sum_{j = 1}^{W_{m}} \nabla_{θ_{m}^{μ}} μ (s_{m}^{j}) \nabla_{a_{m}} Q_{m}^{μ} (s_{m}^{j}, a_{m}^{j}) |}_{a_{m}^{j} = μ (s_{m}^{j})} \end{array}$

算法

在该算法中，联邦学习过程控制了多轮协调。在每一轮中，每一个Agent经过了多次训练，根据其本地数据独立训练其本地模型，而无需了解其他Agent的观察和动作。因此Agent之间没有信息交换，系统的通信开销也显著降低。
在每一轮进行多次训练后，每个Agent将其本地模型的权重上传到MBS（宏基站）就行聚合。联邦平均采用基于小批量的随机梯度下降法：
$\theta^r \gets \sum_m \frac{W_m}{\tilde{W}}\theta_m^r$

$\tilde{W} = \sum_m W_m$：所有Agent的batch size之和。

然后，协调器将平均的全局模型分发回所有Agent让其相应地更新本地模型。或者，模型聚合可以在每个Agent的本地执行。特别是，Agent之间可以通过单元间专用控制通道来交换其模型参数。每个Agent获取所有Agent的模型参数并执行相同的联邦平均操作，这样不同的Age他就可以获得与MBS全局执行的聚合模型相同的模型。此外，相邻的小基站可能经历类似的环境观测，相邻小基站Agent可以聚类成一个合作组来执行模型聚合，降低了通信开销。
尽管actor网络与MARL的网络结构相同，但critic网络的输入大小显著减小，因为只考虑局部状态，而不是所有Agent的状态。因此与MARL相比，联邦DRL的算法复杂度显著降低。

原文地址

Huang, Xiaoyan, et al. “Multi-agent deep reinforcement learning for computation offloading and interference coordination in small cell networks.” IEEE Transactions on Vehicular Technology 70.9 (2021): 9282-9293.